 |
|
|
| |
 |
|
| |
|
|
| |
La fission
|
|
| |
|
|
| |
|
|
| |
|
|
| |
 Calcul
de sections efficaces de fission |
|
| |
|
|
| |
Lorsque l'on cherche à calculer la section efficace de fission induite
par un projectile sur une cible, on
enchaîne plusieurs modèles de réactions nucléaires, décrivant des processus
rapides, intermédiaires et lents. Contrairement aux autres
voies de réactions classiques, la fission résulte
d'une évolution lente du noyau jusqu'à une déformation telle
qu'il se scinde en deux. De ce fait, la section efficace de
fission est obtenue exclusivement par le processus lent du
modèle du noyau composé.
|
|
| |
|
|
| |
Dès lors, des coefficients de transmission doivent être calculés
pour les voies de fission, au même titre que des coefficients
de transmission sont définis pour les voies de réactions classiques.
Comme on l'a vu dans l' approche
théorique, le chemin vers la fission rencontre des obstacles
(barrières) qui peuvent être traversés par effet tunnel. Les coefficients de transmission
représentent donc la probabilité de traverser ces barrières.
|
|
| |
|
|
| |
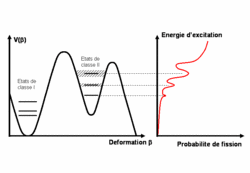
Le calcul de cette probabilité est relativement simple
pour une seule barrière, mais devient plus complexe
quand plusieurs barrières doivent être traversées. En
effet, l'existence de barrières multiples implique l'apparition
de puits entre ces dernières. Or, la présence de puits
de potentiel entraine l'existence d'états dans ce puits,
généralement appelés états de classe II, voire de classe
III dans le cas de trois barrières. De tels états ont
été observés expérimentalement et provoquent un effet
résonant pour le processus de fission, comme l'illustre
la figure ci-contre.
|
|
|
|
Etats de classe II et résonances :
les états de classe II sont indiqués par
les lignes horizontales. Ils induisent des structures
résonantes dans la probabilité de fission. Leur
largeur augmente avec l'énergie d'excitation,
et les pics de résonances sont de ce fait eux
aussi élargis.
|
|
|
 Agrandir le visuel
|
|
|
|
| |
|
|
| |
Cet effet résonnant doit être pris en compte dans le calcul des
sections efficaces de fission car il peut modifier sensiblement
le coefficient de transmission de fission lorsque l'énergie
du système fissionnant est du même ordre de grandeur que celle
des états de classe II ou III.
|
|
| |
|
|
| |
La fission de seconde chance et au-delà
|
|
| |
|
|
| |
Mais la complexité ne s'arrête pas à ce stade. En effet, lorsque
l'énergie du projectile est suffisament élevée, le noyau composé peut
émettre des particules, et c'est alors le noyau résiduel produit qui peut fissionner.
Si le noyau composé initial émet un unique neutron, on parle alors d'une fission de seconde chance.
Dans de telles conditions, la section efficace de fission résulte de
la somme des sections efficaces de fission de tous les noyaux
résiduels pouvant être obtenus après émission de particules
légères. Plus l'énergie du projectile est élevée, plus le
nombre de noyaux susceptibles de fissionner va être important
et donc le nombre de paramètres à ajuster élevé.
|
|
| |
|
|
| |
|
|
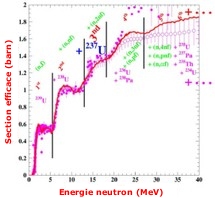
A titre d'illustration, pour un neutron incident de 20 MeV sur
l'uranium 238, il faut connaître non seulement les paramètres
de fission de l'uranium 239 jusqu'à l'uranium 235 (fissions
dite de première chance, seconde, troisième, quatrième et
cinquième chance) mais aussi les paramètres de fission correspondant
aux autres voies énergétiquement ouvertes; pour une telle
énergie incidente; à savoir les voies (n,p), (n,np), (n,d), ...
L'ouverture de telles voies de réaction implique donc de
disposer des paramètres de fission pour les isotopes du protactinium
(crées par l'émission d'un proton) et pour les isotopes du
Thorium (crées par émission d'α).
|
| |
|
|
Section efficace de fission pour
l'uranium 238 en fonction de l'energie du neutron incident.
Les noyaux qu'il est nécessaire de prendre en compte sont indiqués
en rouge et la voie de décroissance qui amène à ces noyaux est
indiquée en vert.
|
|
| |
Agrandir le visuel
|
|
|
| |
|
|
| |
La notion de chances de fission, si elle complique l'évaluation
à haute énergie offre néanmoins un moyen de contrôle de la
cohérence d'ensemble des paramètres de fission. En effet,
lorsque l'on cherche à décrire la fission de l'uranium 238,
les paramètres décrivant la fission de deuxième chance (réaction
(n,nf) ) doivent permettre de décrire aussi la fission de
première chance de l'uranium 237.
|
|
| |
|
|
| |
|
|
De la même manière, la fission
de troisième chance de l'uranium 238 doit correspondre avec
la fission de seconde chance de l'uranium 237 ou encore de
première chance de l'uranium 236. Et la fission de seconde
chance de l'uranium 236 doit être cohérente avec la fission
de première chance de l'uranium 235, mais aussi la quatrième
chance de l'uranium 238. On peut aussi voir la fission de
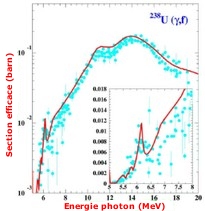
deuxième chance de l'uranium 238 en cohérence avec la photofission
(fission induite par des photons) de l'uranium 238. Cette situation
est illustrée sur la figure ci-contre où l'on voit que
le même jeux de paramètres que ceux utilisés dans
le cas présenté sur la figure précédente permet de bien décrire la
photofission de l'uranium 238.
|
| |
|
|
Section efficace de fission pour
l'uranium 238 en fonction de l'energie du photon incident.
|
|
| |
Agrandir le visuel
|
|
|
| |
|
|
| |
On comprend donc bien que la modélisation de la fission d'un noyau doit
se faire en étudiant simultanément les noyaux voisins, ce
qui implique bien évidemment un travail considérable mais
permet aussi de disposer de données expérimentales supplémentaires
pour ajuster au mieux les divers paramètres de fission.
|
|
| |
|
|
| |
|
|
