 |
|
|
| |
 |
|
| |
|
|
| |
La fission
|
|
| |
|
|
| |
|
|
| |
|
|
| |
 Nature
des fragments de fission et énergie libérée |
|
| |
|
|
| |
Une étude ab initio des distributions de
fragments de fission a été entreprise par le Groupe de structure
nucléaire du Service de Physique Nucléaire de la Direction
des Applications Militaires du CEA. L'objectif est de connaître,
entre autres résultats, les taux de production des produits
de fission.
|
|
| |
|
|
| |
Dans la fission binaire de basse énergie qui nous intéresse actuellement,
la fission apparaît comme un processus lent, qui peut être
schématisé comme un noyau qui s'allonge et se déforme de façon
symétrique ou asymétrique pour se séparer, en fin de compte,
en deux fragments de même masse ou de masses différentes en
un gros fragment et un petit fragment. La connaissance de
la masse des fragments de fission représente "les distributions
en masse des fragments de fission".
|
|
| |
|
|
| |
Dans l'approche utilisée, le noyau est décrit dans un plan
fonction de son élongation et de son asymétrie. Notons que
l'ensemble des points « exits », positions où le système
se casse en deux fragments, constitue ce que l'on appelle
communément la ligne de scission.
|
|
| |
|
|
| |
|
|
Pour chaque couple de déformations (élongation,asymétrie),
l'énergie du système est déterminée et la fission
résulte de l'évolution temporelle d'un paquet
d'onde dans la surface d'énergie potentielle ainsi
obtenue. Les distributions en masse sont calculées
à partir du flux de la fonction d'onde collective
à travers la ligne de scission.
|
| |
|
| |
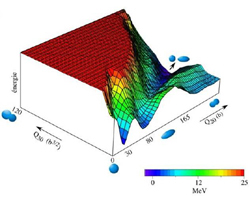
La surface d'énergie potentielle est calculée à l'aide
de la méthode de champ moyen de Hartree-Fock-Bogoliubov
où le seul ingrédient des calculs est la force
d'interaction entre deux nucléons la force effective
D1S développée par D. Gogny. L'exemple fourni
ci-contre, montre la surface d'énergie potentielle
obtenue pour le noyau d'238U en fonction des variables
élongation-asymétrie.
|
| |
Surface d'énergie potentielle de l'238U
|
| |
 Agrandir le visuel
|
|
|
| |
|
|
| |
L'évolution temporelle est réalisée à l'aide de la méthode de la coordonnée
génératrice dépendante du temps. Grâce à l'approximation de
recouvrement gaussien, l'équation à résoudre est une équation
de type Schrödinger à deux dimensions, où les paramètres d'inertie
dépendent des déformations. Le principal avantage de cette
méthode est le fait que le Hamiltonien collectif qui gouverne
l'évolution temporelle est complètement déterminé par les
calculs microscopiques et ne contient pas de paramètres ajustables.
|
|
| |
|
|
| |
|
|
| |
|
|
| |
Modèle statistique de point de scission bas&ecute; sur des ingrédients microscopiques
|
|
| |
|
|
| |
Parallèlement, un autre projet permettant de calculer les distributions en masse et en
charge des fragments de fission est conduit dans le Groupe Modélisation et Evaluation des
Données du Service de Physique Nucléaire de la Direction des Applications Militaires du CEA.
Le but de cette étude est de produire de façon systématique les courbes de distribution en masse,
en excluant tout paramètre phénoménologique, dans le cadre d'un modèle statistique simple. Ces
distributions en masse, non ajustées sur des données expérimentales, pourront ultérieurement
être utilisées dans les codes de calcul des multiplicités des neutrons prompts de fission,
ainsi dans ceux du calcul de leur spectre, qui sont fondamentaux pour la prédiction des réactions
nucléaires en chaîne.
|
|
| |
|
|
| |
L'hypothèse forte du modèle utilisé, dit modèle statique de point de scission, est de considérer
qu'on peut calculer les distributions des fragments de fission à partir d'un seul point de l'évolution
temporelle du système fissionnant, appelé point de scission. L’ "histoire" du système est alors
simulée par l’hypothèse d'équilibre entre les degrés de liberté du système, qui suppose que le
processus de fission est suffisamment lent pour qu’un équilibre thermodynamique soit atteint au
moment où la répartition des nucléons entre chaque fragment est décidée. Au point de scission,
le système fissionnant a une probabilité égale de se trouver dans chaque état quantique accessible
sous les contraintes du système et donc, le rendement d’une paire de fragments donnée ne dépend
que de la densité d’états quantiques.
|
|
| |
|
|
| |
La définition du point de scission est une donnée essentielle du modèle : nous choisissons
de le déterminer à partir des informations obtenues sur le point "exit" dans la description
dynamique totalement microscopique présentée ci-dessus. L’énergie disponible au point de
scission est évaluée au moyen de potentiels microscopiques obtenus à partir d’un calcul
Hartree-Fock-Bogoliubov avec la force D1S de Gogny et nous utilisons pour la densité
d’états une formule de Modèle Superfluide Généralisé.
|
|
|
| |
|
|
Distribution en masse et charge du 226Th.
|
|
| |
Agrandir le visuel
|
|
|
| |
|
|
| |
|
|
|
Les surfaces de distributions de fragments en masse et en charge (figure ci-dessus), permettent
notamment de reproduire correctement l’évolution qualitative du rapport fission asymétrique/fission
symétrique pour les différents isotopes d’actinides et à différentes énergies d’excitation,
comparativement aux résultats expérimentaux (Résultats préliminaires) (figure ci-contre).
|
| |
|
L'utilisation d’un modèle statique, de part sa rapidité en termes de temps de calcul,
permet d’étudier facilement les rendements de fragments pour différents noyaux pères
ou différentes énergies d'excitation, rendant ainsi possible des études systématiques.
|
|
|
|
Evolution de la compétition entre la fission symétrique et
asymétrique pour les isotopes du thorium de A=222 à A=228 :
comparaison entre résultats du calcul (en noir) et l'expérience (en bleu).
|
|
|
|
Agrandir le visuel
|
|
|
|
| |
|
|
| |
|
|
